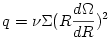Accretion discs/2. Basic physics of accretion discs
From Scholarpedia
| This article has not been published yet; It may be unfinished, contain inaccuracies or unapproved changes. | |||||||||||||||||||||
Author: Dr.
Marek A. Abramowicz, Physics Department, Göteborg University, Sweden
and N. Copernicus Astronomical Center, PAN, Warsaw, Poland
Author: Miss Odele Straub, N. Copernicus Astronomical Center PAN, Warsaw, Poland
Dynamical, thermal and viscous processesThe accretion discs physics is governed by a
non-linear combination of many processes, including gravity,
hydrodynamics, viscosity, radiation and magnetic fields. According to a
semi-analytic understanding of these processes developed over the past
thirty years, the high angular momentum of matter is gradually removed
by viscous stresses and transported outwards. This allows matter in the
accretion disc to gradually spiral down towards the gravity center, with
its gravitational energy degraded to heat. A fraction of the heat
converts into radiation, which partially escapes and cools down the accretion disc.
Accretion disc physics is often described in terms of dynamical,
thermal and viscous processes that occur at different timescales
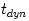 , ,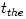 , , 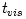 : :
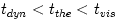 , and in the thin disc analytic models it is assumed that , and in the thin disc analytic models it is assumed that 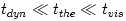 . Although neither these inequalities, nor even the very existence of the separate timescals . Although neither these inequalities, nor even the very existence of the separate timescals 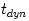 , , 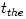 , , 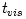 ,
could be considered as well established facts (indeed some of the
supercomputer simulations of accretion seem to challenge that), the
present understanding of the accretion disc physics --- both in general
and in details --- is based (explicitly or implicitly) on this
separation into dynamical, thermal and viscous processes. ,
could be considered as well established facts (indeed some of the
supercomputer simulations of accretion seem to challenge that), the
present understanding of the accretion disc physics --- both in general
and in details --- is based (explicitly or implicitly) on this
separation into dynamical, thermal and viscous processes.
Dynamical processes, with the timescale
|
|
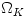 , the radial epicyclic frequency
, the radial epicyclic frequency 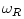 , and the vertical epicyclic frequency
, and the vertical epicyclic frequency 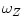 .
They are directly relevant for motion of free particles and also play a
role for determining equilibria and stability of rotating fluids. In
both Newton's and Einstein's gravity the three frequencies are derived
from the effective potential
.
They are directly relevant for motion of free particles and also play a
role for determining equilibria and stability of rotating fluids. In
both Newton's and Einstein's gravity the three frequencies are derived
from the effective potential 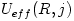 , and given by the same formulae,
, and given by the same formulae,
|
|
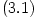 |
where 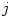 is the specific angular momentum, and derivatives are taken at the symmetry plane
is the specific angular momentum, and derivatives are taken at the symmetry plane 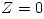 . Small (epicyclic) oscillations around the circular orbit
. Small (epicyclic) oscillations around the circular orbit 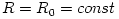 ,
, 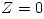 are governed by
are governed by 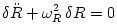 ,
, 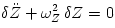 , with solutions
, with solutions 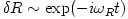 ,
, 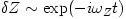 , which are unstable when
, which are unstable when 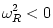 or
or 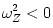 . In Newton's gravity
. In Newton's gravity 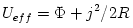 . A spherical Newtonian body has the gravitational potential
. A spherical Newtonian body has the gravitational potential 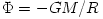 . Thus, in this case,
. Thus, in this case, 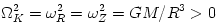 , i.e. all slightly non-circular orbits are closed and all circular orbits are stable.
, i.e. all slightly non-circular orbits are closed and all circular orbits are stable.
In Einstein's gravity, for a spherical body, it is 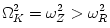 , i.e. non-circular orbits are not closed. In addition, for circular orbits with radii smaller than
, i.e. non-circular orbits are not closed. In addition, for circular orbits with radii smaller than 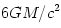 , it is
, it is 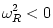 , which indicates the dynamical instability of these orbits. We describe this and other aspects of the black hole gravity that are most relevant to the accretion disc physics in sub-section 2.1 The black hole gravity of this Scholarpedia article.
, which indicates the dynamical instability of these orbits. We describe this and other aspects of the black hole gravity that are most relevant to the accretion disc physics in sub-section 2.1 The black hole gravity of this Scholarpedia article.
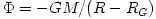 (with
(with 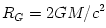 ),
one may accurately describe in Newton's theory the relativistic orbital
motion, and in particular the existence of ISCO. Paczynski's model for
the black hole gravity became a very popular tool in the accretion disc
research. It is used by numerous authors in both analytic and numerical
studies. Effects of special relativity have been added to Paczynski's
model by Abramowicz et al.(1996), and a generalization to a rotating black hole was done by e.g. Karas and Semerak (1999). Newtonian models for rotating black holes are cumbersome and for this reason not widely used, see Abramowicz (2009).
),
one may accurately describe in Newton's theory the relativistic orbital
motion, and in particular the existence of ISCO. Paczynski's model for
the black hole gravity became a very popular tool in the accretion disc
research. It is used by numerous authors in both analytic and numerical
studies. Effects of special relativity have been added to Paczynski's
model by Abramowicz et al.(1996), and a generalization to a rotating black hole was done by e.g. Karas and Semerak (1999). Newtonian models for rotating black holes are cumbersome and for this reason not widely used, see Abramowicz (2009).Viscous processes, with the timescale 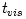
|
Despite the fact that the crucial role of accretion power in quasars and other astrophysical objects was uncovered already forty years ago by Salpeter and Zeldovich, several important aspects of the very nature of accretion discs are still puzzling. One of them is the origin of the viscous stresses. Balbus and Hawley recognized in 1991 that, most probably, viscosity is provided by turbulence, which originates from the magneto-rotational instability. The instability develops when the matter in the accretion disc rotates non-rigidly in a weak magnetic field. There is still no consensus on how strong the resulting viscous stresses are and how exactly they shape the flow patterns in accretion discs. A great part of our detailed theoretical knowledge on the role of this source of turbulence in accretion disc physics comes from numerical supercomputer simulations. The simulations are rather difficult, time consuming, and hardware demanding. Due to mathematical difficulties, in analytic models one does not directly implement a (small scale) magnetohydrodynamical description, but describes the turbulence (or rather the action of a small scale viscosity of an unspecified nature) by a phenomenological "alpha-viscosity prescription" introduced by Shakura and Sunyaev: the kinematic viscosity coefficient is assumed to have the form
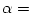 const is a free parameter, const is a free parameter, 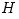 is a lenght scale (usually the pressure scale), and is a lenght scale (usually the pressure scale), and 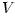 is a characteristic speed (usually the sound speed). There are several
versions of this prescription, the most often used assumes that the
viscous torque
is a characteristic speed (usually the sound speed). There are several
versions of this prescription, the most often used assumes that the
viscous torque 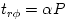 is proportional to a pressure (either the total, or the gas pressure). The rate of viscous dissipation of energy is is proportional to a pressure (either the total, or the gas pressure). The rate of viscous dissipation of energy is |
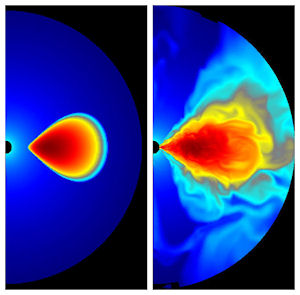
Developement of the MIR instability in a Polish doughnut, from numerical simulations by J. Hawley.
Credit: J.A. Font, Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity |
Thermal processes, with the timescale 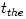
Gravitational and kinetic energy of matter falling onto the central
object is converted by dissipation to heat. Heat is partially radiated
out, partially converted to work on the disc expansion and (in the case
of BH accretion) partially lost inside the hole. The efficiency of
accretion disc 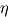 is defined by
is defined by 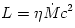 , where
, where 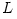 is the total luminosity (power) of the disc radiation. Sołtan
gave a strong observational argument, confirmed and improved later by
other authors, that the efficiency of accretion in quasars is
is the total luminosity (power) of the disc radiation. Sołtan
gave a strong observational argument, confirmed and improved later by
other authors, that the efficiency of accretion in quasars is 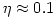 .
Note that the efficiency of thermonuclear reactions inside stars is
about two orders of magnitude smaller. The theoretically predicted
efficiency of geometrically thin and optically thick Shakura-Sunyaev
accretion disc around a black hole is
.
Note that the efficiency of thermonuclear reactions inside stars is
about two orders of magnitude smaller. The theoretically predicted
efficiency of geometrically thin and optically thick Shakura-Sunyaev
accretion disc around a black hole is 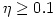 .
Thus, Shakura-Sunyaev accretion discs could explain the enegetics of
the "central engines" of quasars, which are the most efficient steady
engines known in the Universe. Other types of accretion discs models
(like adafs and slim discs) are called the "radiatively inefficient
flows" (RIFs) because they are radiatively much less efficient.
.
Thus, Shakura-Sunyaev accretion discs could explain the enegetics of
the "central engines" of quasars, which are the most efficient steady
engines known in the Universe. Other types of accretion discs models
(like adafs and slim discs) are called the "radiatively inefficient
flows" (RIFs) because they are radiatively much less efficient.
The energy budget may also include rotational energy that could be tapped from the central object. In the black hole case, this possibility was described in a seminal paper by Blandford and Znajek. The Blandford-Znajek process
is an electromagnetic analogy of the well-known Penrose process. Some of its aspects are not yet rigorously described in all relevant physical and mathematical details, and some remain controversial. It is believed that the Blandford-Znajek process may power the relativistic jets.
| > PREVIOUS SECTION 1. Observational evidence... | > FIRST SECTION Scholarpedia Accretion discs | > NEXT SECTION 2.1. The black hole gravity |
| Invited by: | Eugene M. Izhikevich |
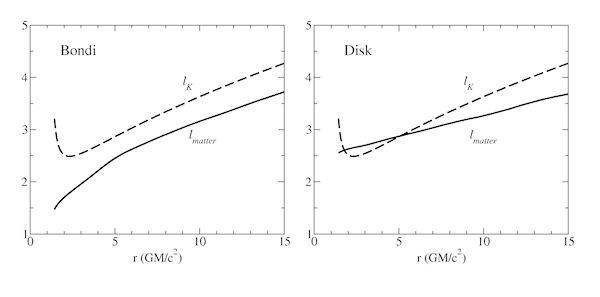
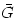 , centrifugal
, centrifugal 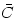 , pressure
, pressure 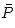 , and magnetic
, and magnetic 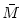 . In particular, accretion discs, are characterized by a significant contribution of
. In particular, accretion discs, are characterized by a significant contribution of 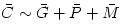 )
in contrast to another important type of accretion flows --- the
quasi-spherical "Bondi" accretion, where the angular momentum is
everywhere smaller than the Keplerian (and therefore dynamically
unimportant,
)
in contrast to another important type of accretion flows --- the
quasi-spherical "Bondi" accretion, where the angular momentum is
everywhere smaller than the Keplerian (and therefore dynamically
unimportant, 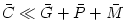 ). Some authors take this difference as a defining condition: in
an "accretion disc" there must be an extended region where the matter's
angular momentum is not smaller than the Keplerian angular momentum in
the same region. This is illustrated in Figure 6.
). Some authors take this difference as a defining condition: in
an "accretion disc" there must be an extended region where the matter's
angular momentum is not smaller than the Keplerian angular momentum in
the same region. This is illustrated in Figure 6. from a spherical object with the mass
from a spherical object with the mass  equals
equals 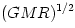 ,
i.e. it is monotonically increasing, indicating (Rayleigh's) stability
of all orbits. According to Einstein's theory, in the strong gravity
near a compact object such as a
,
i.e. it is monotonically increasing, indicating (Rayleigh's) stability
of all orbits. According to Einstein's theory, in the strong gravity
near a compact object such as a 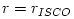 (see Figure 1). All orbits with
(see Figure 1). All orbits with 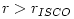 are
are 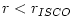 are unstable, the orbit at
are unstable, the orbit at 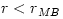 , the unstable orbits are also unbound. For a non-rotating black hole
, the unstable orbits are also unbound. For a non-rotating black hole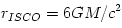 and
and 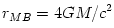 .
.
![\left[ \left(\frac{\partial U_{eff}}{\partial R}\right)_j
= 0\right] \rightarrow \left[ \Omega_K^2 = \Omega_K^2(R) \right],
~~~\omega_R^2(R) = \left(\frac{\partial^2 U_{eff}}{\partial
R^2}\right)_j, ~~~\omega_Z^2(R) = \left(\frac{\partial^2
U_{eff}}{\partial Z^2}\right)_j,](08-basic-physics_files/5fb0d31cb84f68396c2a2572bf286269.png)
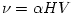 ,
,