|
The black hole gravitational field is described by three parameters: mass 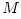 , angular momentum , angular momentum 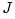 and charge and charge 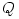 . It is convincingly argued that the astrophysical black holes relevant for accretion discs are uncharged, . It is convincingly argued that the astrophysical black holes relevant for accretion discs are uncharged, 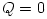 . They are described by the stationary and axially symmetric Kerr geometry, with the metric . They are described by the stationary and axially symmetric Kerr geometry, with the metric 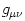 given in the spherical Boyer-Lindquist coordinates given in the spherical Boyer-Lindquist coordinates 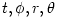 by the explicitly known functions of the radius by the explicitly known functions of the radius 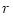 and the polar angle and the polar angle 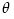 , which are listed in the table below. The table also gives the contravariant form of the metric, , which are listed in the table below. The table also gives the contravariant form of the metric, 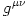 , defined by , defined by 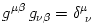 . It is defined, . It is defined, 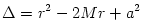 , , 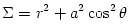 . The signature . The signature 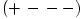 is used. is used.
The mass and angular momentum have been rescaled into the 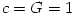 units, units, 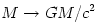 , , 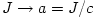 . For a proper black hole solution it must be . For a proper black hole solution it must be 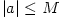 , and the metric with , and the metric with 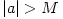 corresponds to a naked singularity. The Penrose cosmic censor
hypothesis (unproved) states that there are no naked singularities in
the Universe.
corresponds to a naked singularity. The Penrose cosmic censor
hypothesis (unproved) states that there are no naked singularities in
the Universe.
In any stationary and axially symmetric spacetime, and in particular in
the Kerr geometry, for matter rotating on circular orbits with four
velocity 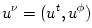 it is it is 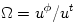 and and 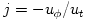 , from which (and , from which (and 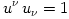 ) it follows that, ) it follows that,
|
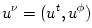 it is
it is 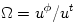 and
and 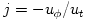 , from which (and
, from which (and 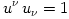 ) it follows that,
) it follows that,
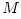 , angular momentum
, angular momentum 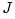 and charge
and charge 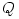 . It is convincingly argued that the astrophysical black holes relevant for accretion discs are uncharged,
. It is convincingly argued that the astrophysical black holes relevant for accretion discs are uncharged, 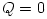 . They are described by the stationary and axially symmetric Kerr geometry, with the metric
. They are described by the stationary and axially symmetric Kerr geometry, with the metric 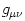 given in the spherical Boyer-Lindquist coordinates
given in the spherical Boyer-Lindquist coordinates 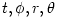 by the explicitly known functions of the radius
by the explicitly known functions of the radius 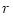 and the polar angle
and the polar angle 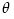 , which are listed in the table below. The table also gives the contravariant form of the metric,
, which are listed in the table below. The table also gives the contravariant form of the metric, 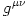 , defined by
, defined by 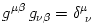 . It is defined,
. It is defined, 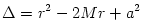 ,
, 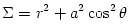 . The signature
. The signature 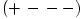 is used.
is used.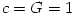 units,
units, 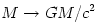 ,
, 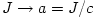 . For a proper black hole solution it must be
. For a proper black hole solution it must be 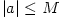 , and the metric with
, and the metric with 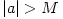 corresponds to a naked singularity. The Penrose cosmic censor
hypothesis (unproved) states that there are no naked singularities in
the Universe.
corresponds to a naked singularity. The Penrose cosmic censor
hypothesis (unproved) states that there are no naked singularities in
the Universe.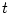
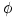
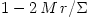
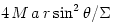
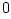
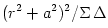
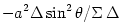
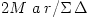
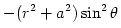
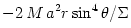
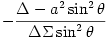
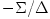
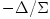
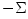
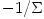
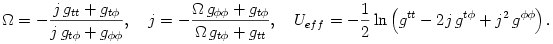
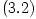
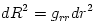 ,
, 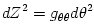 , one derives that the Keplerian frequency
, one derives that the Keplerian frequency 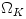 and the two epicyclic frequencies (radial
and the two epicyclic frequencies (radial  and vertical
and vertical  ) equal
) equal
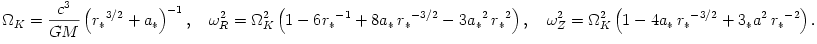
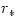 and
and 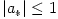 are defined by
are defined by 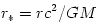 ,
, 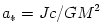 . In the strong gravity, i.e. for
. In the strong gravity, i.e. for 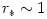 , the three frequencies scale as
, the three frequencies scale as 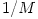 . The radial epicyclic oscillations,
. The radial epicyclic oscillations, 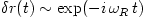 , become dynamically unstable at
, become dynamically unstable at 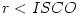 , because there
, because there 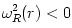 .
.