Thick discs: assumptions
For "thick discs" models of accretion discs one assumes that:
- Matter distribution is stationary and axially symmetric, i.e. matter quantities such as density
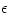 or pressure or pressure 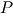 are independent on time are independent on time 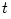 and the azimuthal angle and the azimuthal angle 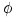 . .
- Matter moves on circular trajectories, i.e. the four velocity has the form
![u^i = [u^t, u^{\phi}, 0, 0]](14-thick_files/4b4fa54a4669e6474b93627c15441a5f.png) . The angular velocity is defined as . The angular velocity is defined as 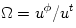 , and the angular momentum as , and the angular momentum as 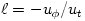 , ,
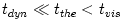 , with , with 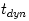 being the dynamical timescale in which pressure force adjusts to the balance of gravitational and centrifugal forces, being the dynamical timescale in which pressure force adjusts to the balance of gravitational and centrifugal forces, 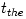 being the thermal timescale in which the entropy redistribution occurs due to dissipative heating and cooling processes, and being the thermal timescale in which the entropy redistribution occurs due to dissipative heating and cooling processes, and 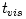 being the viscous timescale in which angular momentum distribution
changes due to torque caused by dissipative stresses. Mathematically,
this is equivalent to assume the stress-energy tensor in the form,
being the viscous timescale in which angular momentum distribution
changes due to torque caused by dissipative stresses. Mathematically,
this is equivalent to assume the stress-energy tensor in the form, 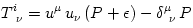 . .
Using this form of the stress-energy tensor, Abramowicz et al. 1978 have derived from the equilibrium condition 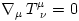 the relativistic "Euler" equation,
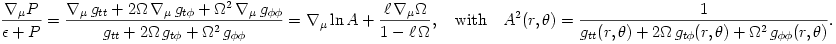
|
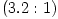 |
Equipressure surfaces: analytic solution in a general case
The "equipressure" surfaces are defined by an implicit condition  , which may be solved to get the explicit form  . Then, (3.2:1) implies that the function 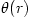 obeys, If 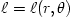 or, which is equivalent, 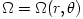 are known functions, the equation (3.2:2) for the equipressure surfaces takes the form of a standard ordinary differential equation 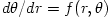 with known rhs, and it may be directly integrated. This has been done first by Jaroszynski et al., 1980 and then by several other authors. In the Figure below, we show an example from a recent paper by Lei et al., 2008 who assumed the angular momentum distribution in the form that depends on three constant parameters ( 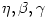 ),
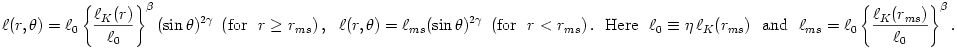
|
 |
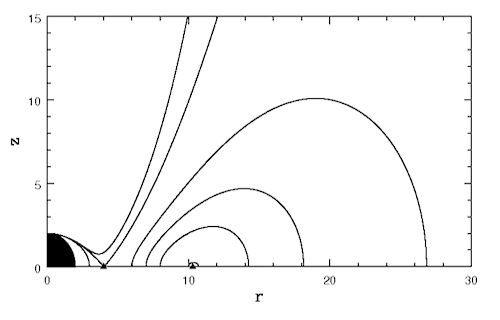
Fig. 1 Equipressure surfaces for a non rotating black hole, and with angular momentum distribution (3.2:3) with 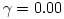 , 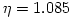 , 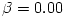 . Angular momentum is constant everywhere in space.
|
|
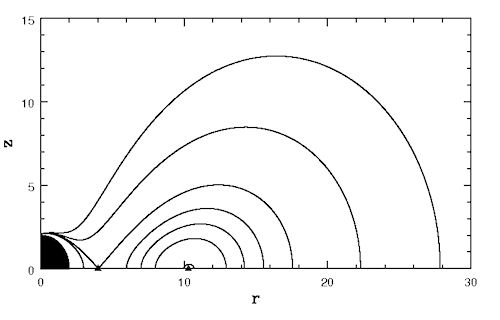
Fig. 2 Equipressure surfaces for a non rotating black hole, and with angular momentum distribution (3.2:3) with 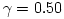 , 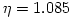 , 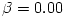 . Angular momentum is constant radially, but it changes along the polar angle.
|
|
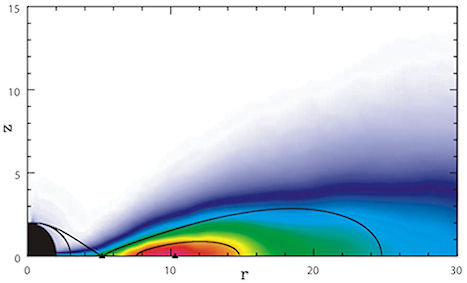
Fig. 3 Equipressure surfaces for a non rotating black hole, and with angular momentum distribution (3.2.3) with 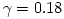 , 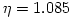 , 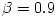 , compared with global MHD numerical simulations by Fragile et al., 2007, time averaged over a period corresponding to the orbital period at 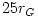 (color-coded).
|
|
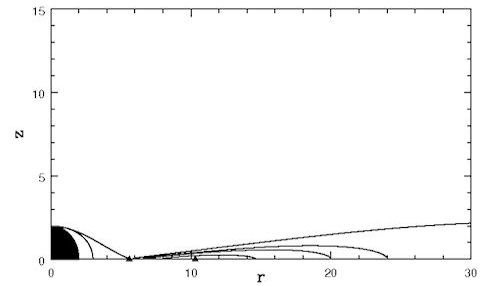
Fig. 4 Equipressure surfaces for a non rotating black hole, and with angular momentum distribution (3.2.3) with 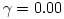 , 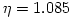 , 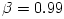 . Angular momentum does not depend on the polar angle, its radial distribution is almost Keplerian.
|
|
Barytropic thick discs and the von Zeipel theorem
From equation (3.1:1) one proves (see e.g. Abramowicz et al. 1978) that for barytropic fluids 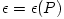 , the surfaces of constant angular velocity and of constant angular momentum coincide, i.e. 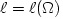 . This is often called "the von Zeipel theorem". The equation of state 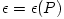 and the rotation law 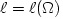 are independent and may be separately assumed. When they are known, the analytic solution is given by, The functions 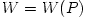 , 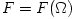 and 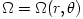 are explicitly known, and therefore one knows explicitly location of the equipressure surfaces 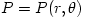 . In the special (but important) case 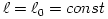 , the function 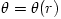 that gives the location of equipressure surfaces 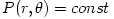 is given explicitly (for a non-rotating black hole) Putting 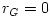 in (3.2:5), one recovers the Newtonian formula for 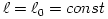 discs in the 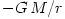 potential. The Roche lobe overflow
|
|
Fig. 5 Taken from Abramowicz et al., 1980 (a) At the location 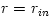 , called the "cusp", angular momentum in the disc equals the Keplerian one, 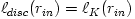 . For 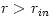 it is 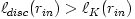 and 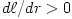 , and for 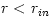 it is 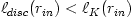 and 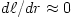 . (b) The particular equipotential surface 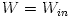 , called the "Roche lobe", crosses itself at the cusp. For 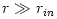 the surface of the disc ( 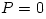 ) coincides with the equipotential 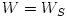 . (c) The non-zero potential difference 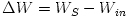
implies that no equilibrium is possible at radii around and smaller
than the cusp. Instead, there will be dynamical mass loss from the disk
with the accretion rate that for a polytropic fluid 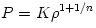 equals ( Kozlowski et al. 1978, Abramowicz 1985)
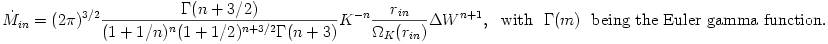
|
 |
The mass loss (3.2:5) induced by the Roche lobe
overflow self-regulates the accretion rate in the innermost part of all
types of accretion disks (thin, slim, adafs, thick) around black holes
and sufficiently compact neutron stars. This self-regulated overflow has
several important consequences:
- It locally stabilizes accretion discs against thermal and viscous instabilities (Abramowicz, 1981) and globally against the Papaloizou and Pringle instability (Blaes, 1987)
- The amount of overflow, and therefore
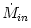 ,
may be modulated by global discs oscillations. In the case of neutron
stars, this leads to a modulation of the luminosity of the boundary
layer at the neutron star surface. Although oscillations originate in
the disk, the are observed in radiation that comes from the boundary
layer. This is relevant for the observed neutron star quasi periodic
oscillation (QPO) (Horak et al., 2007). ,
may be modulated by global discs oscillations. In the case of neutron
stars, this leads to a modulation of the luminosity of the boundary
layer at the neutron star surface. Although oscillations originate in
the disk, the are observed in radiation that comes from the boundary
layer. This is relevant for the observed neutron star quasi periodic
oscillation (QPO) (Horak et al., 2007).
- The "runaway" instability occurs when the mass exchange between
accretion disc and black hole causes the cusp to move deeper into the
disc, increasing the mass lost rate
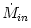 . This effect was suggested by Abramowicz et al. (1983), and studied by several other authors (e.g. Daigne and Font, 2004 or Montero et al., 2008). It may determine the life-time of a massive torus around a black hole, which is relevant to some models of gamma ray bursts. . This effect was suggested by Abramowicz et al. (1983), and studied by several other authors (e.g. Daigne and Font, 2004 or Montero et al., 2008). It may determine the life-time of a massive torus around a black hole, which is relevant to some models of gamma ray bursts.
|
|
|
Fig. 6 Taken from Igumenshchev and Beloborodov, 1997. The analytic formula (3.2:5) is very accurate, as a comparison with the numerical simulations shows. (a)
The numerically calculated equipressure structure close to the central
black hole is remarkably similar to that calculated analytically. In
particular, there is obviously a cusp there. (b) In a qualitative
agreement with the analytic model, the radial fluid velocity (described
by arrows) is small far away from the cusp 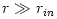 , but large (no equilibrium) at 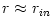 . (c)
Even more impressive is the excellent quantitative agreement of the
predictions of the analytic formula (3.2:5), represented by lines, with
results of numerical simulations, represented by points (circles,
squares and triangles).
|
Super-Eddington luminosities of radiation pressure supported thick discs ("Polish doughnuts")
The maximal energy available from an object with the mass 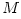 (and gravitational radius 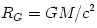 ) is 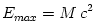 . The minimal time in which this energy may be liberated is 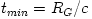 . Thus, the maximal power ![L_{max} = E_{max}/t_{min} = c^5/G \equiv L_{Planck} = 10^{58}\,[{\rm erg/sec}] = 10^{52}\,[{\rm Watts}]](14-thick_files/e665c61d44f4903edbc9564794f399fe.png) . An object with mass 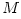 has the "gravitational cross-section" 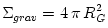 . If radiation interacts with matter by electron scattering (with the Thomson cross section 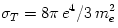 ), its "radiation cross section" is 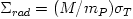 .
M. Sikora noticed (unpublished) that the upper limit for the
radiative power of an object in which gravity and radiation pressure are
in equilibrium is given by the Planck power and the object
gravitational and radiative cross sections,
![(\,\rm{Eddington~luminosity}\,) \equiv L_{Edd} = L_{Planck}\frac{\Sigma_{grav}}{\Sigma_{rad}} = \frac{4\pi\,G\,M\,m_P\,c}{\sigma_T}
= 1.4 \times 10^{38}\left( \frac{M}{M_{sun}}\right) [{\rm erg}/{\rm sec}].](14-thick_files/8a2fc7c2b68d80751af8b7d2fe13382b.png)
|
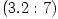 |
 |
|
A "Polish doughnut" is a radiation pressure
supported thick accretion discs around a central black hole. Polish
doughnuts have toroidal shapes, resembling a large sphere ( 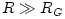 ) with a pair of empty narrow funnels along the rotation axis. The total luminosity of a Polish doughnut may be approximated as 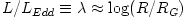 . The logarithm here is of a crucial importance. It prevents astrophysically realistic doughnuts (i.e. with 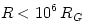 ,
say) to have highly super-Eddington luminosities. The theory predicts
for such "realistic" fat tori slightly super-Eddington total (isotropic)
luminosities 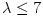 . However, because the funnels have solid angles 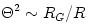 , radiation in the funnels may be, in principle, collimated to highly super-Eddington values 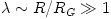 . This simple estimate agrees with a more detailed modeling of the Polish doughnuts radiation field by Sikora (1981) and Madau (1988) who obtained 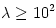 for discs with 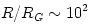 . A typical value that follows from observational estimates for the non-blazar active galactic nuclei, e.g. by Czerny and Elvis (1987) is 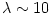 ,
but of course for blazars and other similar sources (e.g. for ULXs, if
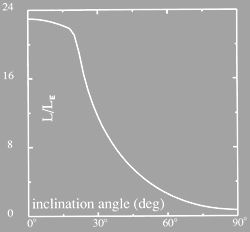
they are powered by stellar mass black holes, as argued e.g. by King (2008), it must be  . Fig. 7 (Credit: Madau (1988)) shows radiation from a Polish doughnut seen at different inclination angles, inclination 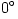 corresponds to line of sight along the funnel axis. |
![(\,\rm{Eddington~accretion~rate}\,) \equiv {\dot M}_{Edd} = \frac{L_{Edd}}{c^2}
= 1.5 \times 10^{17}\left( \frac{M}{M_{sun}}\right) [{\rm g}/{\rm sec}], ~~~{\dot m} = \frac{\dot M}{{\dot M}_{Edd}}.](14-thick_files/e5e7634d8e8131cc65e83580b6e07e25.png)
|
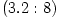 |
Theoretical predictions about super-Eddington accretion rates:
- Radiation pressure supported black hole thick accretion discs ("Polish doughnuts") have typically super-Eddington luminosities
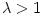 . .
- These discs have very small accretion efficiency and therefore must have highly super-Eddington accretion rates
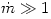 . .
- Super-Eddington accretion does not necessarily imply strong outflows.
The assumption that 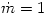
is the upper limit for the growth rate of the seed black holes, often
adopted in the context of the cosmic structure formation, is false. |
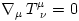 the relativistic "Euler" equation,
the relativistic "Euler" equation,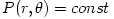 , which may be solved to get the explicit form
, which may be solved to get the explicit form 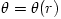 . Then, (3.2:1) implies that the function
. Then, (3.2:1) implies that the function 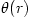 obeys,
obeys,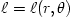 or, which is equivalent,
or, which is equivalent, 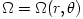 are known functions, the equation (3.2:2) for the equipressure surfaces takes the form of a standard ordinary differential equation
are known functions, the equation (3.2:2) for the equipressure surfaces takes the form of a standard ordinary differential equation 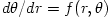 with known rhs, and it may be directly integrated. This has been done first by Jaroszynski et al., 1980 and then by several other authors. In the Figure below, we show an example from a recent paper by Lei et al., 2008 who assumed the angular momentum distribution in the form that depends on three constant parameters (
with known rhs, and it may be directly integrated. This has been done first by Jaroszynski et al., 1980 and then by several other authors. In the Figure below, we show an example from a recent paper by Lei et al., 2008 who assumed the angular momentum distribution in the form that depends on three constant parameters (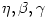 ),
), , the surfaces of constant angular velocity and of constant angular momentum coincide, i.e.
, the surfaces of constant angular velocity and of constant angular momentum coincide, i.e. 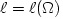 . This is often called "the von Zeipel theorem". The equation of state
. This is often called "the von Zeipel theorem". The equation of state 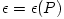 and the rotation law
and the rotation law 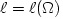 are independent and may be separately assumed. When they are known, the analytic solution is given by,
are independent and may be separately assumed. When they are known, the analytic solution is given by,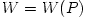 ,
, 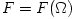 and
and 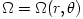 are explicitly known, and therefore one knows explicitly location of the equipressure surfaces
are explicitly known, and therefore one knows explicitly location of the equipressure surfaces 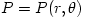 . In the special (but important) case
. In the special (but important) case 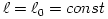 , the function
, the function 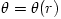 that gives the location of equipressure surfaces
that gives the location of equipressure surfaces 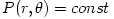 is given explicitly (for a non-rotating black hole)
is given explicitly (for a non-rotating black hole)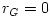 in (3.2:5), one recovers the Newtonian formula for
in (3.2:5), one recovers the Newtonian formula for 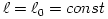 discs in the
discs in the 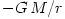 potential.
potential.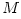 (and gravitational radius
(and gravitational radius 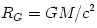 ) is
) is 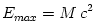 . The minimal time in which this energy may be liberated is
. The minimal time in which this energy may be liberated is 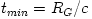 . Thus, the maximal power
. Thus, the maximal power ![L_{max} = E_{max}/t_{min} = c^5/G \equiv L_{Planck} = 10^{58}\,[{\rm erg/sec}] = 10^{52}\,[{\rm Watts}]](14-thick_files/e665c61d44f4903edbc9564794f399fe.png) . An object with mass
. An object with mass 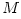 has the "gravitational cross-section"
has the "gravitational cross-section" 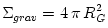 . If radiation interacts with matter by electron scattering (with the Thomson cross section
. If radiation interacts with matter by electron scattering (with the Thomson cross section 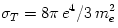 ), its "radiation cross section" is
), its "radiation cross section" is 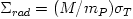 .
M. Sikora noticed (unpublished) that the upper limit for the
radiative power of an object in which gravity and radiation pressure are
in equilibrium is given by the Planck power and the object
gravitational and radiative cross sections,
.
M. Sikora noticed (unpublished) that the upper limit for the
radiative power of an object in which gravity and radiation pressure are
in equilibrium is given by the Planck power and the object
gravitational and radiative cross sections,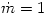 is the upper limit for the growth rate of the seed black holes, often
adopted in the context of the cosmic structure formation, is false.
is the upper limit for the growth rate of the seed black holes, often
adopted in the context of the cosmic structure formation, is false.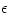 or pressure
or pressure 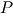 are independent on time
are independent on time 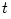 and the azimuthal angle
and the azimuthal angle 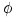 .
.![u^i = [u^t, u^{\phi}, 0, 0]](14-thick_files/4b4fa54a4669e6474b93627c15441a5f.png) . The angular velocity is defined as
. The angular velocity is defined as 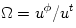 , and the angular momentum as
, and the angular momentum as 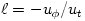 ,
,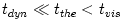 , with
, with 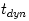 being the dynamical timescale in which pressure force adjusts to the balance of gravitational and centrifugal forces,
being the dynamical timescale in which pressure force adjusts to the balance of gravitational and centrifugal forces, 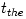 being the thermal timescale in which the entropy redistribution occurs due to dissipative heating and cooling processes, and
being the thermal timescale in which the entropy redistribution occurs due to dissipative heating and cooling processes, and 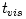 being the viscous timescale in which angular momentum distribution
changes due to torque caused by dissipative stresses. Mathematically,
this is equivalent to assume the stress-energy tensor in the form,
being the viscous timescale in which angular momentum distribution
changes due to torque caused by dissipative stresses. Mathematically,
this is equivalent to assume the stress-energy tensor in the form, 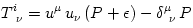 .
.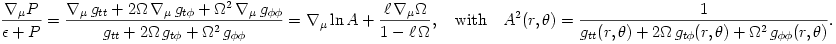
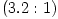
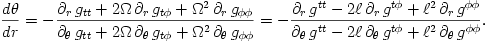
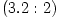
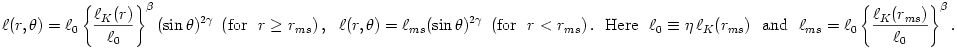
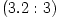

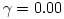 ,
, 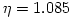 ,
, 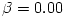 . Angular momentum is constant everywhere in space.
. Angular momentum is constant everywhere in space.
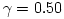 ,
, 
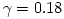 ,
, 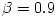 , compared with global
, compared with global 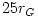 (color-coded).
(color-coded).
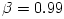 . Angular momentum does not depend on the polar angle, its radial distribution is almost Keplerian.
. Angular momentum does not depend on the polar angle, its radial distribution is almost Keplerian.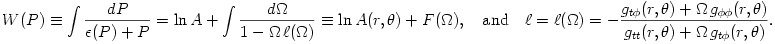
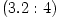
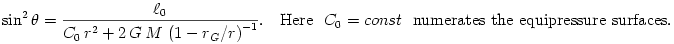
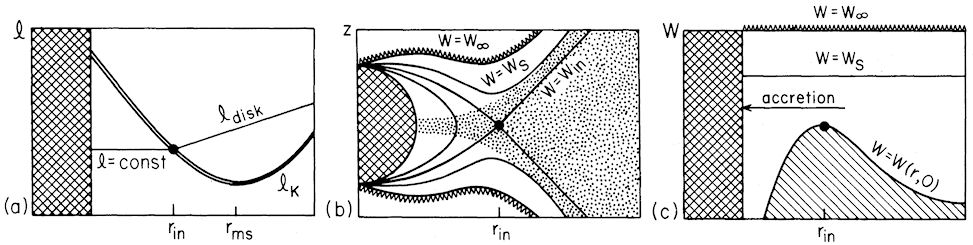
 , called the "cusp", angular momentum in the disc equals the Keplerian one,
, called the "cusp", angular momentum in the disc equals the Keplerian one, 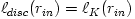 . For
. For 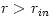 it is
it is 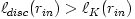 and
and 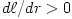 , and for
, and for 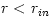 it is
it is 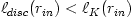 and
and 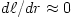 . (b) The particular equipotential surface
. (b) The particular equipotential surface 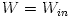 , called the "Roche lobe", crosses itself at the cusp. For
, called the "Roche lobe", crosses itself at the cusp. For 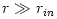 the surface of the disc (
the surface of the disc (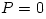 ) coincides with the equipotential
) coincides with the equipotential 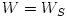 . (c) The non-zero potential difference
. (c) The non-zero potential difference 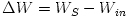 implies that no equilibrium is possible at radii around and smaller
than the cusp. Instead, there will be dynamical mass loss from the disk
with the accretion rate that for a polytropic fluid
implies that no equilibrium is possible at radii around and smaller
than the cusp. Instead, there will be dynamical mass loss from the disk
with the accretion rate that for a polytropic fluid 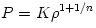 equals (
equals (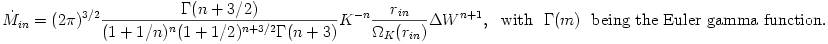
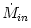 ,
may be modulated by global discs oscillations. In the case of neutron
stars, this leads to a modulation of the luminosity of the boundary
layer at the neutron star surface. Although oscillations originate in
the disk, the are observed in radiation that comes from the boundary
layer. This is relevant for the observed neutron star quasi periodic
oscillation (QPO)
,
may be modulated by global discs oscillations. In the case of neutron
stars, this leads to a modulation of the luminosity of the boundary
layer at the neutron star surface. Although oscillations originate in
the disk, the are observed in radiation that comes from the boundary
layer. This is relevant for the observed neutron star quasi periodic
oscillation (QPO) 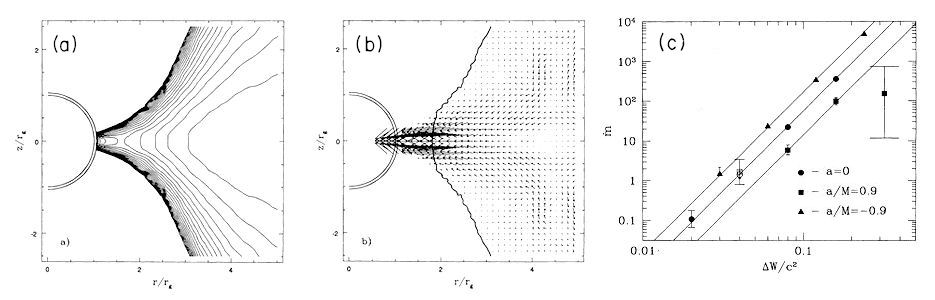
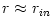 . (c)
Even more impressive is the excellent quantitative agreement of the
predictions of the analytic formula (3.2:5), represented by lines, with
results of numerical simulations, represented by points (circles,
squares and triangles).
. (c)
Even more impressive is the excellent quantitative agreement of the
predictions of the analytic formula (3.2:5), represented by lines, with
results of numerical simulations, represented by points (circles,
squares and triangles).![(\,\rm{Eddington~luminosity}\,) \equiv L_{Edd} = L_{Planck}\frac{\Sigma_{grav}}{\Sigma_{rad}} = \frac{4\pi\,G\,M\,m_P\,c}{\sigma_T}
= 1.4 \times 10^{38}\left( \frac{M}{M_{sun}}\right) [{\rm erg}/{\rm sec}].](14-thick_files/8a2fc7c2b68d80751af8b7d2fe13382b.png)
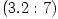

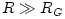 ) with a pair of empty narrow funnels along the rotation axis. The total luminosity of a Polish doughnut may be approximated as
) with a pair of empty narrow funnels along the rotation axis. The total luminosity of a Polish doughnut may be approximated as 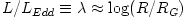 . The logarithm here is of a crucial importance. It prevents astrophysically realistic doughnuts (i.e. with
. The logarithm here is of a crucial importance. It prevents astrophysically realistic doughnuts (i.e. with 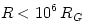 ,
say) to have highly super-Eddington luminosities. The theory predicts
for such "realistic" fat tori slightly super-Eddington total (isotropic)
luminosities
,
say) to have highly super-Eddington luminosities. The theory predicts
for such "realistic" fat tori slightly super-Eddington total (isotropic)
luminosities 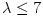 . However, because the funnels have solid angles
. However, because the funnels have solid angles 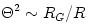 , radiation in the funnels may be, in principle, collimated to highly super-Eddington values
, radiation in the funnels may be, in principle, collimated to highly super-Eddington values 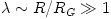 . This simple estimate agrees with a more detailed modeling of the Polish doughnuts radiation field by
. This simple estimate agrees with a more detailed modeling of the Polish doughnuts radiation field by 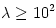 for discs with
for discs with 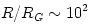 . A typical value that follows from observational estimates for the non-blazar active galactic nuclei, e.g. by
. A typical value that follows from observational estimates for the non-blazar active galactic nuclei, e.g. by 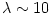 ,
but of course for blazars and other similar sources (e.g. for ULXs, if
they are powered by stellar mass black holes, as argued e.g. by
,
but of course for blazars and other similar sources (e.g. for ULXs, if
they are powered by stellar mass black holes, as argued e.g. by  . Fig. 7 (Credit:
. Fig. 7 (Credit: 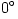 corresponds to line of sight along the funnel axis.
corresponds to line of sight along the funnel axis.![(\,\rm{Eddington~accretion~rate}\,) \equiv {\dot M}_{Edd} = \frac{L_{Edd}}{c^2}
= 1.5 \times 10^{17}\left( \frac{M}{M_{sun}}\right) [{\rm g}/{\rm sec}], ~~~{\dot m} = \frac{\dot M}{{\dot M}_{Edd}}.](14-thick_files/e5e7634d8e8131cc65e83580b6e07e25.png)
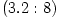
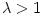 .
.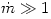 .
.