Expansion in the "smallness" prameter. The "global" parameters of a thin disc: mass, accretion rate, viscosity
Most of the analytic and semi-analytic accretion disc models assume that the disc is stationary and axially symmetric.
"Thin" disc models assume in addition that the vertical extension of
the disk is small in a general sense that in cylindrical coordinates 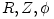 the disc surface is given by the disc surface is given by 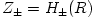 and and 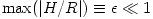 . Here . Here 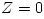 describes the location of the accretion disc plane. In the spherical coordinates the plane is given by describes the location of the accretion disc plane. In the spherical coordinates the plane is given by 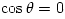 , and the condition of the small vertical extension by , and the condition of the small vertical extension by 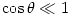 everywhere inside the disc. everywhere inside the disc.
The thin disc models are based on expanding the hydrodynamical (or MHD) equations in powers of 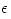 .
The expansion procedure is not unique, and depends on some extra
physical assumptions made. It leads to equations of the general form 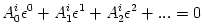 . For most models, the resulting set of equations, 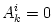 , consists of a number of coupled, linear first-order ordinary differential equations (containing 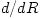
derivatives) and a few non-linear algebraical equations. Usually, the
integration constants may be associated with (and calculated from) the
three "global" parameters of thin disc models that are the mass of the
central accreting object 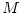 , the accretion rate 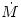 , and the viscosity parameter 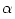 .
The "standard thin", "adaf" and "slim" disc equations
Newtonian hydrodynamical models of stationary and
axially symmetric, thin accretion discs are described by equations
similar to (or equivalent to) the 12 equations given in the table below.
A "model" should give each of the 12 unknown quantities, for example
the matter density 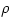 , as a function of the radius 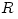 , and the three model parameters 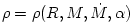 .
| Equations |
|
Unknown functions |
| (01) |
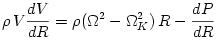 |
radial balance of forces |
|
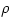 |
density of matter |
| (02) |
![{\dot M}\left[ \frac{dU}{dR} + P\,\frac{d}{dR}\left(\frac{1}{\rho}\right)\right]
= 4\pi R^2 H(\tau_{R \phi}) \frac{d\Omega}{dR} + 4\pi R\,F](16-thin_files/e9d8f88744b6692293f7ff5b2994cb8b.png) |
energy conservation |
|
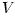 |
radial velocity |
| (03) |
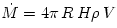 |
mass conservation |
|
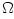 |
angular velocity of matter |
| (04) |
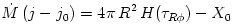 |
angular momentum conservation |
|
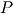 |
pressure |
| (05) |
![F = \frac{acT^{4}}{[\kappa\,\rho\,H]}](16-thin_files/684c39812e8465700d1590daa079a524.png) |
vertical radiative transfer |
|
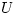 |
internal energy (thermodynamics) |
| (06) |
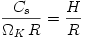 |
vertical momentum balance |
|
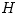 |
vertical thickness |
| (07) |
![(\tau_{R\phi}) = \rho[\alpha\,C_s\,H]R\frac{d\Omega}{dR}](16-thin_files/1b36fa6c89ef0e5c4af52e86cba3ba37.png) |
"viscous" torque 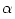 prescription prescription |
|
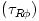 |
viscous torque |
| (08) |
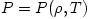 |
equation of state |
|
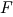 |
flux of radiation |
| (09) |
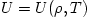 |
equation of state (internal energy) |
|
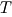 |
temperature |
| (10) |
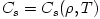 |
equation of state (sound speed) |
|
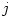 |
angular momentum |
| (11) |
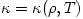 |
opacity |
|
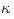 |
opacity coefficient |
| (12) |
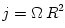 |
angular momentum and angular velocity |
|
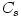 |
sound speed |
NOTE:
these equations are valid for the standard Shakura-Sunyaev discs, for
adafs and for slin discs. In the case of the standard Shakura-Sunyaev
discs further assumptions are made, which transform all the equations to
the algebraical ones. Specifically, in equation (01) one puts 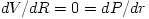 which leads to 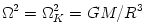 . In equation (02) one puts 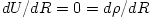 which leads, after some manipulations involving other equations, to
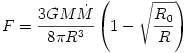
This is the famous Shakura-Sunyaev flux formula. Note also that the
gravitation field of the central object enters the above Newtonian
equations only through the Keplerian angular velocity 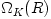 .
In the general relativistic version of (01)-(12) the gravity (i.e. the
spacetime curvature) enters also through components of the metric tensor
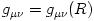 the equatorial plane. The Kerr geometry version of (01)-(12) was written first by Lasota (1994), and later elaborated by Abramowicz, Chen, Granath and Lasota (1996); see also Sadowski (2009)..
However, equations (01)-(12) in their form above are often used to
model the black hole accretion discs. This is possible because of a
brilliant discovery by Paczynski of the Newtonian model for the black hole gravity.
Particular models make several additional simplifying assumptions. For example, several models assume that 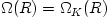 , with , with 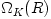 being the Keplerian angular velocity, which is known since the
gravitational field of the central object is known (for a spherical body
with the mass
being the Keplerian angular velocity, which is known since the
gravitational field of the central object is known (for a spherical body
with the mass 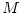 Newton's theory yields Newton's theory yields 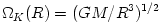 ). Note, that in this case the derivative ). Note, that in this case the derivative 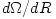 that appears in equations (02) and (07) becomes a known function of that appears in equations (02) and (07) becomes a known function of 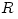 . Equation (07) postulates the form of the "viscous" stress . Equation (07) postulates the form of the "viscous" stress 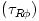 in therms of an ad hoc ansatz that introduces the dimensionless in therms of an ad hoc ansatz that introduces the dimensionless 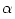 -viscosity.
Note that the quantity that appears in square bracket is called in
hydrodynamics the "kinematic viscosity". The original Shakura-Sunyaev
ansatz postulated -viscosity.
Note that the quantity that appears in square bracket is called in
hydrodynamics the "kinematic viscosity". The original Shakura-Sunyaev
ansatz postulated 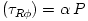 .
Equation (05) gives the flux of radiation in (a very rough) diffusion
approximation. Note that the quantity in square brackets in this
equation is the optical depth, .
Equation (05) gives the flux of radiation in (a very rough) diffusion
approximation. Note that the quantity in square brackets in this
equation is the optical depth, ![\tau = [\kappa\,\rho\,H]](16-thin_files/4b314cd4ce21458398f3a7e7d8b35fa6.png) in the vertical direction. The equation is valid only if in the vertical direction. The equation is valid only if 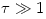 , and if , and if 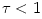 non-thermal radiative processes should be considered, and equation (05) replaced by non-thermal radiative processes should be considered, and equation (05) replaced by 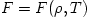 . .
In equation (04), 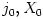 are the angular momentum and the viscous torque at some undefined radius are the angular momentum and the viscous torque at some undefined radius 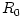 . In the black hole accretion discs models, it is customary to take . In the black hole accretion discs models, it is customary to take 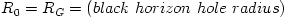 , because the viscus torque at the horizon vanishes. Then, , because the viscus torque at the horizon vanishes. Then, 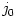 is the (a priori unknown) angular momentum of matter at the horizon.
With respect to first order derivatives, quations (01)-(12) form a
linear system that may be solved for each derivative. For
is the (a priori unknown) angular momentum of matter at the horizon.
With respect to first order derivatives, quations (01)-(12) form a
linear system that may be solved for each derivative. For 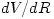 this gives, this gives,
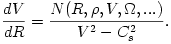
Any black hole accretion flow must be transonic, i.e. somewhere it must pass the sonic radius 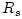 , where , where 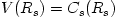 . In order that . In order that 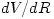 and all other derivatives are non-singular there, it must be, and all other derivatives are non-singular there, it must be,
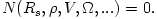
The above sonic point regularity condition makes the system (01)-(12)
over constrained, i.e. an eigenvalue problem, with the eigenvalue being
the angular momentum at the horizon, 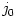 . .
Analytic models describe black hole accretion discs down to a certain "inner edge" 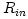 which locates close to the central accreting object. The inner edge is a
theoretical concept introduced for convenience, because at
which locates close to the central accreting object. The inner edge is a
theoretical concept introduced for convenience, because at 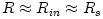 the accretion flow changes its character. In the case of the black hole
accretion, the change goes from almost circular orbits to almost radial
free fall. It is therefore convenient to separately model the two
regions:
the accretion flow changes its character. In the case of the black hole
accretion, the change goes from almost circular orbits to almost radial
free fall. It is therefore convenient to separately model the two
regions: 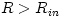 where matter moves on circular orbits, and where matter moves on circular orbits, and 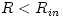 where matter free falls. Of course, in reality the situation is more
complicated, as the change of the flow character occurs smoothly in an
extended region on both sides of
where matter free falls. Of course, in reality the situation is more
complicated, as the change of the flow character occurs smoothly in an
extended region on both sides of 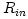 . For black hole accretion, . For black hole accretion, 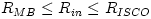 . For very efficient Shakura-Sunyaev discs, . For very efficient Shakura-Sunyaev discs, 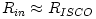 , while for RIFs , while for RIFs 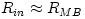 . For stellar accretion, . For stellar accretion, 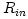 is located near the surface of the star and the flow there is described by a boundary layer model. For more details on the inner edge of a thin disk, see Abramowicz, Jaroszynski, Kato and Sadowski (2009) and references quoted there. is located near the surface of the star and the flow there is described by a boundary layer model. For more details on the inner edge of a thin disk, see Abramowicz, Jaroszynski, Kato and Sadowski (2009) and references quoted there.
The "standard" model: Shakura-Sunyaev
|
Characteristic, applications, references
|
Analytic formulae (solution)
|
Axially symmetric, stationary, local analytic model. Explicit formulae give all physical characteristics in terms of 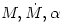 and and 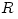 . It is geometrically thin in the vertical direction . It is geometrically thin in the vertical direction 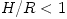 ,
and has a disc-like shape. Accretion rate is very sub-Eddington.
Opacity is very high. The gas goes down on tight spirals, approximated
by circular, free (Keplerian, geodesic) orbits. For black hole and (very
compact) neutron star the inner edge locates at ISCO. High luminosity,
high efficiency of radiative cooling. Electromagnetic spectra is not
much different from that of a sum of black bodies. Alpha viscosity
prescription assuned. Diffusion approximation for radiative transfer
used. It is dynamically stable.
When the gas is cold and radiation pressure negligible, it is also
thermally and viscously stable, otherwise it is unstable in both
respects. ,
and has a disc-like shape. Accretion rate is very sub-Eddington.
Opacity is very high. The gas goes down on tight spirals, approximated
by circular, free (Keplerian, geodesic) orbits. For black hole and (very
compact) neutron star the inner edge locates at ISCO. High luminosity,
high efficiency of radiative cooling. Electromagnetic spectra is not
much different from that of a sum of black bodies. Alpha viscosity
prescription assuned. Diffusion approximation for radiative transfer
used. It is dynamically stable.
When the gas is cold and radiation pressure negligible, it is also
thermally and viscously stable, otherwise it is unstable in both
respects.
Applications: YSOs, CVs, LMXRB, AGNs. The best known and studied theoretical model.
Standard reference: Shakura, Sunyaev (1974) , one of the most often quoted papers in modern astrophysics (quotation counts).
Similar ideas: Pringle, Rees (1972); Lynden-Bell, Pringle (1974)
Fully relativistic version (Novikov, Thorne 1974); for the detailed description see: Page, Thorne (1974). Recent application to spectral fits: Shafee et al. (2006); Middleton et al. (2006).
Recommended review: Pringle (1981).
|
Different analytic solutions are known for cases in which the total pressure is either dominated by gas or radiation pressure, and for the opacity described either by Kramers' law, or electron scattering.
However, the most important formula that gives the locally emitted flux
of radiation does not depend on these physical conditions, and is
universally given (in Newton's theory) by,
The Newtonian formulae below correspond to the case of gas pressure and Kramers' law opacity law
![H = 1.7\times 10^8\alpha^{-1/10}\dot{M}^{3/20}_{16} m_1^{-3/8} R^{9/8}_{10}f^{3/5} {\rm [cm]}](16-thin_files/2ca91e95f4ff00bd777cb3633bec6712.png)
![T = 1.4\times 10^4 \alpha^{-1/5}\dot{M}^{3/10}_{16} m_1^{1/4} R^{-3/4}_{10}f^{6/5}{\rm [K]}](16-thin_files/a69cebf2c2ea1ad6656ff83a6d6a9d09.png)
![\rho = 3.1\times 10^{-8}\alpha^{-7/10}\dot{M}^{11/20}_{16} m_1^{5/8} R^{-15/8}_{10}f^{11/5}{\rm [g\ cm}^{-3}{\rm]}](16-thin_files/2fe401f63de9dab613e5942921129ce8.png)
Here 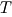 and and 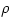 are the mid-plane temperature and density respectively. are the mid-plane temperature and density respectively. 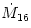 is the accretion rate, in units of is the accretion rate, in units of ![10^{16}{\rm [g\ s]}^{-1}](16-thin_files/2b74484b3c820cc153a51e36ed783ed3.png) , , 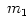 is the mass of the central accreting object in units of a solar mass, is the mass of the central accreting object in units of a solar mass, 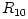 is the radial location in the disc, in units of is the radial location in the disc, in units of ![10^{10}{\rm [cm]}](16-thin_files/769693dc117f5ac8234f40d730b651ed.png) , and , and ![f = [1-(R_0/R)^{1/2}]^{1/4}](16-thin_files/49cd1c381ea4666f8d204fa29f26cac6.png) , where , where 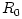 is the inner radius of the disc. is the inner radius of the disc.
|
Notes:
The flux formula in the box is (probably) the most often used one in
the accretion disc research. It shows that the flux does not depend on 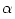 , the viscosity parameter. Other physical quantities depend on 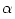 rather weakly. This which is a very fortunate feature of the Shakura-Sunyaev model, as the 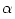 -viscosity prescription is assumed ad hoc and not derived from the first principles.
Specific versions (and modifications) of the Shakura-Sunyaev models
S-curves and the thermal-viscous instability:
The standard accretion discs are known to be subject to thermal-viscous
instability due to the partial hydrogen ionization. As a result of this
instability, the disk cycles between two states: a hot and mostly
ionized state with a large local accretion rate and a cold, neutral
state with a low accretion rate. This instability was originally
proposed to explain the large-amplitude luminosity variations observed
in cataclysmic variables (Smak 1982; Meyer & Meyer-Hofmeister 1982). It is also believed that the same mechanism is responsible for the eruptions in soft X-ray transients (see, e.g. Cannizzo, Ghosh, & Wheeler 1982; Dubus, Hameury, & Lasota 2001; and Lasota 2001
for a review). The ionization instability was also shown to operate in
the disks around supermassive black holes in active galactic nuclei (Lin & Shields 1986; Clarke 1988; Mineshige & Shields 1990; Siemiginowska, Czerny, & Kostyunin 1996). The characteristic timescales of cycle activity scale roughly with the mass of a compact object (Hatziminaoglou, Siemiginowska, & Elvis 2001).
Therefore, the observed cycle timescale of the order of years in
binaries translates into thousands to millions of years in galaxies that
harbor a supermassive black hole.
Warped and precessing discs: A geometrically thin, optically thick accretion disk is unstable to self-induced warping when illuminated by a sufficiently strong central radiation source (Pringle 1996; Maloney, Begelman, & Pringle 1996; see also Petterson 1977).
The instability is important for the standard (not advectively
dominated) discs around neutron stars and black holes in the X-ray
binaries, in active galactic nuclei (Pringle 1997), and in particular in the "maser" galaxy NGC 4258 (Maloney, Begelman, & Pringle 1996).
For disks around less compact objects, where efficiency is orders of
magnitude smaller, steady disks are predicted to be stable. The warped
discs are important in some models of the (~kilohertz) coherent
oscillations (QPOs) observed in neutron star and black hole X-ray
binaries. In the Schwarzschild metric, the damping or excitation of
g-modes with azimuthal dependence 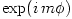 has been considered by Kato (2003, 2004, 2005, 2007),
who found that m = 0, 1 modes undergo resonant amplification when
interacting with a nonrotating one-armed (m = 1) stationary warp,
assumed to be present in the accretion disk. Description of the warp
instability here is based on Armitage & Pringle 1997. See a critical examination of the idea e.g. in Ivanov & Papaloizou 2008. has been considered by Kato (2003, 2004, 2005, 2007),
who found that m = 0, 1 modes undergo resonant amplification when
interacting with a nonrotating one-armed (m = 1) stationary warp,
assumed to be present in the accretion disk. Description of the warp
instability here is based on Armitage & Pringle 1997. See a critical examination of the idea e.g. in Ivanov & Papaloizou 2008.
Magnetized discs:
Self-gravitating discs:
Saturn's rings:
ADAFs
|
Characteristic, applications, references
|
Radial distributions
|
Sub-Eddington accretion, very small opacity. Adafs are cooled by
advection (heat captured by moving matter) rather than by radiation.
They are very radiatively inefficient, geometrically extended, similar
in shape to a sphere (or a "corona") rather than a disc, and very hot
(close to the virial temperature). Because of their low efficiency,
adafs are much less luminous than the Shakura-Sunyaev thin discs. Adafs
emit a power-law,
non-thermal radiation, often with a strong Compton component. For black
hole and (very compact) neutron star the inner edge at a radius smaller
than ISCO. Dynamically, thermally and viscously stable.
Applications: mostly LMXRB, AGNs, with good fits to observed spectra.
Numerical 1.5D (vertically integrated) stationary transonic models (in Kerr): Abramowicz et al. (1996); Narayan et al. (1997); Popham, Gammie (1998) Numerical 2D non-stationary models (in Paczynski-Wiita): Igumenshev et al. (1996).
Most influential paper, describing a Newtonian, self-similar, stationary, axially symmetric analytic, model: Narayan, Yi (1994). Immediate follow-up by the same group: Narayan, Yi (1995); Narayan, Mahadevan (1995); Narayan et al. (1996).
The idea mentioned first time: Ichimaru (1987), see also: Rees et al. (1982); Abramowicz et al. (1995).
Recommended review: Narayan, McClintock (2008).
|
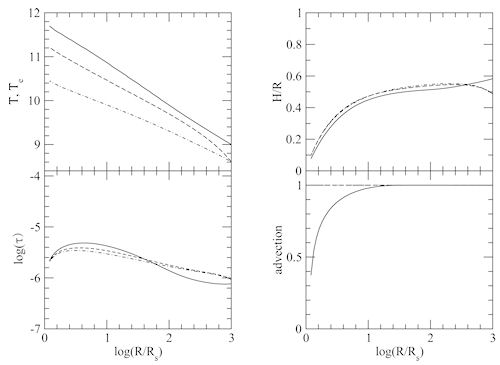
The profiles of temperature, optical depth, ratio
of scale height to radius, and the advection factor of a hot
one-temperature accretion solution (solid lines). The parameters are: 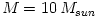 , 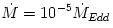 , 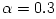 , 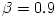 . The outer boundary conditions are 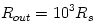 , 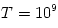 [K], 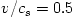 .
For simplicity, effects associated with outflow or convection are not
taken into account. The two-temperature solutions with the same
parameters and 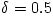 (dashed lines) and 0.01 (dot-dashed lines) are also shown for comparison. Figure credit: Yuan, Taam, Xue, Cui (2006) |
Specific versions (and modifications) of the adaf models
Convection: cadafs
Outflows: adios
Magnetized adafs
Slim discs
|
Characteristic, applications, references
|
The local flux
|
Nearly Eddington accretion. Large opacity. Cooled
by radiation and advection, i.e. heat trapped in matter and transported
towards the central accretor. Radiatively much less efficient than the
standard Shakura-Sunyaev discs. 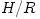
only slightly less than one. For black hole and (very compact) neutron
star the inner edge at a radius smaller than ISCO. Dynamically,
thermally and viscously stable. Rotation differs (slightly but
importantly) from the Keplerian one. The pressure gradient along the
disc plane direction is dynamically important. Slim discs models are
described by a set of ordinary differential equations, and one must
explicitly solve the eigenvalue problem connected with the regularity
condition at the sonic radius (which does not coincide with the ISCO).
Applications: mostly LMXRB, AGNs, ULX. For detailed spectral fits see e.g.:
- Most sophisticated slim disc models (in the Kerr geometry): Sadowski (2009)
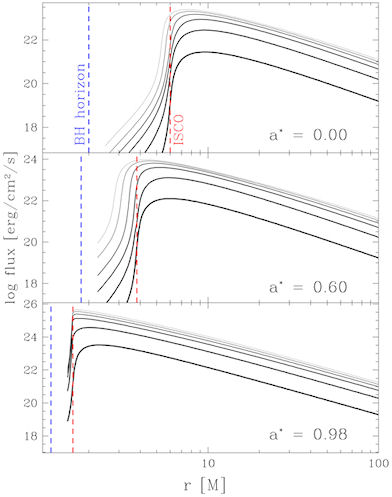
Figure on the right shows the local flux of
radiation for different mass accretion rates and the black hole spins.
Each subplot contains six solid lines for the following mass accretion
rates (in the Eddington units): 0.01 (the thickest line), 0.1, 0.3, 0.6
and 0.9 (the thinnest line). The upper panel is for a non rotating blach
hole (a = 0), the middle one for (a = 0.6) while the bottom one for a
highly spinning black hole (a = 0.98). The black hole mass is 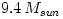 . NOTE that a considerable amount of energy is radiated inside the ISCO; this is an effect of advection. Figure credit: Sadowski (2009)
|
|
Kluzniak-Kita
Fully two dimensional analytic solution (stationary, axially
symmetric) obtained through a mathematically exact expansion in the
small parameter H/R of the equations of viscous hydrodynamics.
Significant backflows in the midplane of the disk have been found.
Kluzniak, Kita (2000), numerical follow up: Umurhan et al. (2006).
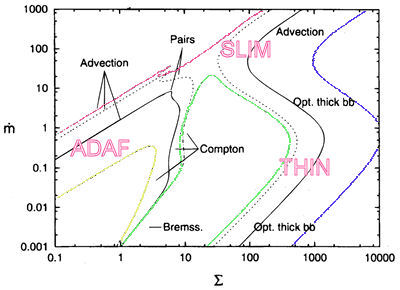
All thin disc solutions
Lines correspond to fixed M, r, and 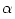 .
An example of each of the four branches is shown in a corresponding
color: pink, blue, green, and yellow. The congruence of all branches has
a critical point, corresponding to .
An example of each of the four branches is shown in a corresponding
color: pink, blue, green, and yellow. The congruence of all branches has
a critical point, corresponding to 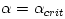 .
In different places of the parameter space, the cooling is dominated by
black body radiation, bremsstrahlung, Compton losses, pair production,
or by advection, as indicated by arrows. Figure adapted from Björnsson et al. (1996). .
In different places of the parameter space, the cooling is dominated by
black body radiation, bremsstrahlung, Compton losses, pair production,
or by advection, as indicated by arrows. Figure adapted from Björnsson et al. (1996).
Branch I (blue): Shakura-Sunyaev (gas pressure) + Shakura-Sunyaev (radiation pressure) + Slim.
Branch II (green): Shakura-Sunyaev (gas pressure) + SLE
Branch III (yellow): SLE + Adaf.
Branch IV (pink): Polish doughnut.
|
|
|
|
|
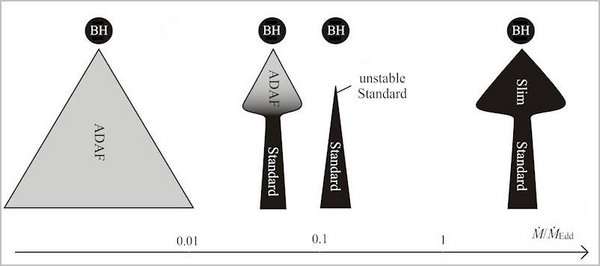
The different types of thin discs may coexist radially.
Microquasaes display distinct spectral states. In order of increasing
luminosity these are the quiescent state, low state, intermediate state,
high state, and very high state. Narayan with collaborators presented a
model of accretion flows around black holes that unifies most of these
states. At low mass accretion rates, the inner ADAF zone in the model
radiates extremely inefficiently, and the outer thin disk is restricted
to large radii. The luminosity therefore is low, and this configuration
is identified with the quiescent state. For larger accretion rates the
radiative efficiency of the ADAF increases rapidly and the system
becomes fairly luminous. The spectrum is very hard and peaks around 100
keV. This is the low state. For still greater rates, the ADAF
progressively shrinks in size, the transition radius decreases, and the
X-ray spectrum changes continuously from hard to soft. This is the
intermediate state. Finally, the inner ADAF zone disappears altogether
and the thin accretion disc extends down to the marginally stable orbit.
The spectrum is dominated by an ultrasoft component with a weak hard
tail. This is the high state.
|
|
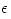 .
The expansion procedure is not unique, and depends on some extra
physical assumptions made. It leads to equations of the general form
.
The expansion procedure is not unique, and depends on some extra
physical assumptions made. It leads to equations of the general form 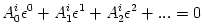 . For most models, the resulting set of equations,
. For most models, the resulting set of equations,  , consists of a number of coupled, linear first-order ordinary differential equations (containing
, consists of a number of coupled, linear first-order ordinary differential equations (containing 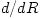 derivatives) and a few non-linear algebraical equations. Usually, the
integration constants may be associated with (and calculated from) the
three "global" parameters of thin disc models that are the mass of the
central accreting object
derivatives) and a few non-linear algebraical equations. Usually, the
integration constants may be associated with (and calculated from) the
three "global" parameters of thin disc models that are the mass of the
central accreting object 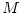 , the accretion rate
, the accretion rate 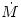 , and the viscosity parameter
, and the viscosity parameter 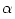 .
.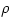 , as a function of the radius
, as a function of the radius 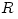 , and the three model parameters
, and the three model parameters 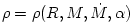 .
.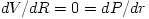 which leads to
which leads to 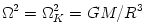 . In equation (02) one puts
. In equation (02) one puts 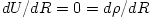 which leads, after some manipulations involving other equations, to
which leads, after some manipulations involving other equations, to
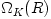 .
In the general relativistic version of (01)-(12) the gravity (i.e. the
spacetime curvature) enters also through components of the metric tensor
.
In the general relativistic version of (01)-(12) the gravity (i.e. the
spacetime curvature) enters also through components of the metric tensor
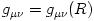 the equatorial plane. The Kerr geometry version of (01)-(12) was written first by Lasota (1994), and later elaborated by Abramowicz, Chen, Granath and Lasota (1996); see also Sadowski (2009)..
However, equations (01)-(12) in their form above are often used to
model the black hole accretion discs. This is possible because of a
brilliant discovery by Paczynski of the Newtonian model for the black hole gravity.
the equatorial plane. The Kerr geometry version of (01)-(12) was written first by Lasota (1994), and later elaborated by Abramowicz, Chen, Granath and Lasota (1996); see also Sadowski (2009)..
However, equations (01)-(12) in their form above are often used to
model the black hole accretion discs. This is possible because of a
brilliant discovery by Paczynski of the Newtonian model for the black hole gravity.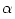 , the viscosity parameter. Other physical quantities depend on
, the viscosity parameter. Other physical quantities depend on 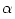 rather weakly. This which is a very fortunate feature of the Shakura-Sunyaev model, as the
rather weakly. This which is a very fortunate feature of the Shakura-Sunyaev model, as the 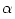 -viscosity prescription is assumed ad hoc and not derived from the first principles.
-viscosity prescription is assumed ad hoc and not derived from the first principles.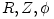 the disc surface is given by
the disc surface is given by 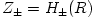 and
and 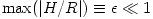 . Here
. Here 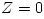 describes the location of the accretion disc plane. In the spherical coordinates the plane is given by
describes the location of the accretion disc plane. In the spherical coordinates the plane is given by 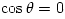 , and the condition of the small vertical extension by
, and the condition of the small vertical extension by 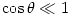 everywhere inside the disc.
everywhere inside the disc.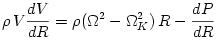
![{\dot M}\left[ \frac{dU}{dR} + P\,\frac{d}{dR}\left(\frac{1}{\rho}\right)\right]
= 4\pi R^2 H(\tau_{R \phi}) \frac{d\Omega}{dR} + 4\pi R\,F](16-thin_files/e9d8f88744b6692293f7ff5b2994cb8b.png)
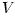
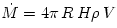
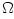
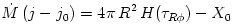
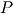
![F = \frac{acT^{4}}{[\kappa\,\rho\,H]}](16-thin_files/684c39812e8465700d1590daa079a524.png)
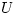
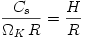
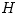
![(\tau_{R\phi}) = \rho[\alpha\,C_s\,H]R\frac{d\Omega}{dR}](16-thin_files/1b36fa6c89ef0e5c4af52e86cba3ba37.png)
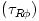
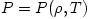
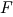
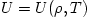
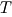
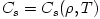
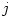
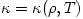
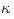
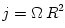
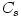
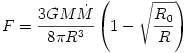
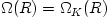 , with
, with 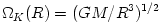 ). Note, that in this case the derivative
). Note, that in this case the derivative 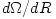 that appears in equations (02) and (07) becomes a known function of
that appears in equations (02) and (07) becomes a known function of 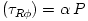 .
Equation (05) gives the flux of radiation in (a very rough) diffusion
approximation. Note that the quantity in square brackets in this
equation is the optical depth,
.
Equation (05) gives the flux of radiation in (a very rough) diffusion
approximation. Note that the quantity in square brackets in this
equation is the optical depth, ![\tau = [\kappa\,\rho\,H]](16-thin_files/4b314cd4ce21458398f3a7e7d8b35fa6.png) in the vertical direction. The equation is valid only if
in the vertical direction. The equation is valid only if 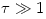 , and if
, and if 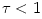 non-thermal radiative processes should be considered, and equation (05) replaced by
non-thermal radiative processes should be considered, and equation (05) replaced by 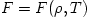 .
.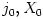 are the angular momentum and the viscous torque at some undefined radius
are the angular momentum and the viscous torque at some undefined radius  . In the black hole accretion discs models, it is customary to take
. In the black hole accretion discs models, it is customary to take 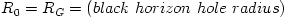 , because the viscus torque at the horizon vanishes. Then,
, because the viscus torque at the horizon vanishes. Then, 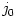 is the (a priori unknown) angular momentum of matter at the horizon.
With respect to first order derivatives, quations (01)-(12) form a
linear system that may be solved for each derivative. For
is the (a priori unknown) angular momentum of matter at the horizon.
With respect to first order derivatives, quations (01)-(12) form a
linear system that may be solved for each derivative. For 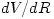 this gives,
this gives,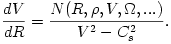
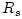 , where
, where 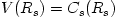 . In order that
. In order that 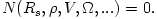
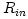 which locates close to the central accreting object. The inner edge is a
theoretical concept introduced for convenience, because at
which locates close to the central accreting object. The inner edge is a
theoretical concept introduced for convenience, because at 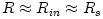 the accretion flow changes its character. In the case of the black hole
accretion, the change goes from almost circular orbits to almost radial
free fall. It is therefore convenient to separately model the two
regions:
the accretion flow changes its character. In the case of the black hole
accretion, the change goes from almost circular orbits to almost radial
free fall. It is therefore convenient to separately model the two
regions: 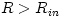 where matter moves on circular orbits, and
where matter moves on circular orbits, and 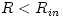 where matter free falls. Of course, in reality the situation is more
complicated, as the change of the flow character occurs smoothly in an
extended region on both sides of
where matter free falls. Of course, in reality the situation is more
complicated, as the change of the flow character occurs smoothly in an
extended region on both sides of 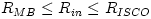 . For very efficient Shakura-Sunyaev discs,
. For very efficient Shakura-Sunyaev discs, 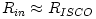 , while for RIFs
, while for RIFs 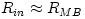 . For stellar accretion,
. For stellar accretion, 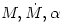 and
and 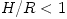 ,
and has a disc-like shape. Accretion rate is very sub-Eddington.
Opacity is very high. The gas goes down on tight spirals, approximated
by circular, free (Keplerian, geodesic) orbits. For black hole and (very
compact) neutron star the inner edge locates at ISCO. High luminosity,
high efficiency of radiative cooling. Electromagnetic spectra is not
much different from that of a sum of black bodies. Alpha viscosity
prescription assuned. Diffusion approximation for radiative transfer
used. It is dynamically
,
and has a disc-like shape. Accretion rate is very sub-Eddington.
Opacity is very high. The gas goes down on tight spirals, approximated
by circular, free (Keplerian, geodesic) orbits. For black hole and (very
compact) neutron star the inner edge locates at ISCO. High luminosity,
high efficiency of radiative cooling. Electromagnetic spectra is not
much different from that of a sum of black bodies. Alpha viscosity
prescription assuned. Diffusion approximation for radiative transfer
used. It is dynamically ![H = 1.7\times 10^8\alpha^{-1/10}\dot{M}^{3/20}_{16} m_1^{-3/8} R^{9/8}_{10}f^{3/5} {\rm [cm]}](16-thin_files/2ca91e95f4ff00bd777cb3633bec6712.png)
![T = 1.4\times 10^4 \alpha^{-1/5}\dot{M}^{3/10}_{16} m_1^{1/4} R^{-3/4}_{10}f^{6/5}{\rm [K]}](16-thin_files/a69cebf2c2ea1ad6656ff83a6d6a9d09.png)
![\rho = 3.1\times 10^{-8}\alpha^{-7/10}\dot{M}^{11/20}_{16} m_1^{5/8} R^{-15/8}_{10}f^{11/5}{\rm [g\ cm}^{-3}{\rm]}](16-thin_files/2fe401f63de9dab613e5942921129ce8.png)
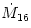 is the accretion rate, in units of
is the accretion rate, in units of ![10^{16}{\rm [g\ s]}^{-1}](16-thin_files/2b74484b3c820cc153a51e36ed783ed3.png) ,
, 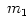 is the mass of the central accreting object in units of a solar mass,
is the mass of the central accreting object in units of a solar mass, 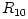 is the radial location in the disc, in units of
is the radial location in the disc, in units of ![10^{10}{\rm [cm]}](16-thin_files/769693dc117f5ac8234f40d730b651ed.png) , and
, and ![f = [1-(R_0/R)^{1/2}]^{1/4}](16-thin_files/49cd1c381ea4666f8d204fa29f26cac6.png) , where
, where 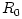 is the inner radius of the disc.
is the inner radius of the disc.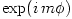 has been considered by Kato (
has been considered by Kato (
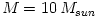 ,
, 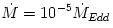 ,
, 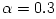 ,
, 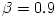 . The outer boundary conditions are
. The outer boundary conditions are 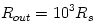 ,
, 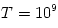 [K],
[K], 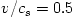 .
For simplicity, effects associated with outflow or convection are not
taken into account. The two-temperature solutions with the same
parameters and
.
For simplicity, effects associated with outflow or convection are not
taken into account. The two-temperature solutions with the same
parameters and 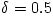 (dashed lines) and 0.01 (dot-dashed lines) are also shown for comparison. Figure credit:
(dashed lines) and 0.01 (dot-dashed lines) are also shown for comparison. Figure credit: 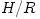 only slightly less than one. For black hole and (very compact) neutron
star the inner edge at a radius smaller than ISCO. Dynamically,
thermally and viscously stable. Rotation differs (slightly but
importantly) from the Keplerian one. The pressure gradient along the
disc plane direction is dynamically important. Slim discs models are
described by a set of ordinary differential equations, and one must
explicitly solve the eigenvalue problem connected with the regularity
condition at the sonic radius (which does not coincide with the ISCO).
only slightly less than one. For black hole and (very compact) neutron
star the inner edge at a radius smaller than ISCO. Dynamically,
thermally and viscously stable. Rotation differs (slightly but
importantly) from the Keplerian one. The pressure gradient along the
disc plane direction is dynamically important. Slim discs models are
described by a set of ordinary differential equations, and one must
explicitly solve the eigenvalue problem connected with the regularity
condition at the sonic radius (which does not coincide with the ISCO).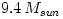 . NOTE that a considerable amount of energy is radiated inside the ISCO; this is an effect of advection. Figure credit:
. NOTE that a considerable amount of energy is radiated inside the ISCO; this is an effect of advection. Figure credit: 
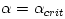 .
In different places of the parameter space, the cooling is dominated by
black body radiation, bremsstrahlung, Compton losses, pair production,
or by advection, as indicated by arrows. Figure adapted from
.
In different places of the parameter space, the cooling is dominated by
black body radiation, bremsstrahlung, Compton losses, pair production,
or by advection, as indicated by arrows. Figure adapted from